[Boston Key Party CTF 2017] qt crackme (rev 250)
Задание: bkp-cutie-keygen.zip
Как следует из названия это будет что-то написанное на Qt, и да, мы получаем ехе-шник с кучей библиотек и прочего шлака. Ну, хорошо что не статически собранный файл, так хоть можно все Qt-шные функции видеть. Обилием которых можно “насладится” с самых первых секунд анализа. Функция main пестрит ими, а в добавок видим, что тут еще Qml используется, становится еще “веселее”.
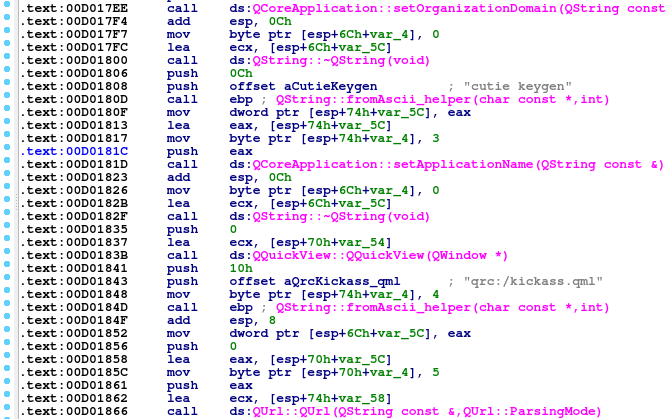
Среди этого всего есть только одна интересная функция sub_D01BF0, которая инициализирует какие-то данные.
Сам crackme представляет с себя окошко с избыточными эффектами, которое принимает ключ в 16 символов.
Решил посмотреть что же написано в kickass.qml. Немного поискав нашел утилиту, которая может доставать ресурсы Qt приложений. Она была написана под .NET, кажется на F# и она не отработала, т.к. мне не знаком был тот синтаксис на котором оно было написано, я не смог разобраться, что же не работает и как пофиксить. И решил прибегнуть к радикальным методам, а именно к binwalk :) и он справился, он достал мне qml файл. В нем не нашел ничего интересного, да я и не знал, что же там может быть, никогда до этого с ним не сталкивался.
Решено было изучить само приложение лучше и была найдена многообещающая функция с выводом отладочных сообщений. По сообщениям было просто найти функцию, которая отвечала за проверку ключа. Разбирать это все в статике было больно, декомпилятор позволял понять общий ход, какая функция что принимает и что и куда отдает дальше, но сами алгоритмы не особо то и понимались. Забегая наперед можно сказать, что это все из-за того что была работа с 64 битной арифметикой в 32 битном приложении. Потому отладка могла разъяснить многие моменты.
.text:00D01DB3 call ds:QString::QString(QString const &) ; password
.text:00D01DB9 mov ecx, ebx
.text:00D01DBB call xor_passwd
.text:00D01DC0 push eax
.text:00D01DC1 lea ecx, [esp+128h+arg_0]
.text:00D01DC8 call ds:QString::operator=(QString const &)
.text:00D01DCE push ecx
.text:00D01DCF lea eax, [esp+12Ch]
.text:00D01DD6 mov ecx, esp
.text:00D01DD8 push eax
.text:00D01DD9 call ds:QString::QString(QString const &)
.text:00D01DDF mov ecx, ebx
.text:00D01DE1 call encrypt_passwd ; work with xored password
Поначалу все просто, ключ ксорится с данными, которые инициализировались еще в самом начале, о чем я выше писал:
.text:00D0221B mov [esp+0B4h+var_24], 70BC90DFh
.text:00D02226 mov [esp+0B4h+var_20], 5A96EF57h
.text:00D02231 mov [esp+0B4h+var_1C], 5509CFEEh
.text:00D0223C mov [esp+0B4h+var_18], 0D2080CEh
.text:00D02247 mov [esp+0B4h+var_14], 70EE14Fh
.text:00D02252 mov [esp+0B4h+var_10], 2FC6A446h
.text:00D0225D mov [esp+0B4h+var_C], 5355ECF0h
.text:00D02268 mov [esp+0B4h+var_8], 6457782Bh
Далее идет функция, которая шифрует поксореный ключ. Сперва она пересохраняет элементы в big endian, для того что бы работать с ключом не посимвольно, а как с единым блоком данных. Сам алгоритм шифрования блочный, он работает с парой блоков по 64 бита, также использует пару ключей по 64 бит каждый. Эти же ключи также инициализируются в само начале как и тот что для ксора:
.text:00D022B8 mov dword ptr [edi+18h], 880F0E3Ah
.text:00D022BF mov dword ptr [edi+1Ch], 16D856AFh
.text:00D022C6 mov dword ptr [edi+20h], 58FF310h
.text:00D022CD mov dword ptr [edi+24h], 0D8E8367Ch
Вот алгоритм шифрования пожалуй самое интересное. Т.к. он работает с данными по 64 бита, а 32 битное приложение не может оперировать такими блоками, оно обрабатывает их по очереди по 32 бита по этому можно почти половину инструкций игнорить, если понимать что это продолжение предыдущей операции.
.text:00D029C0 loc_D029C0: ; CODE XREF: encrypt_passwd+409
.text:00D029C0 xor eax, eax
.text:00D029C2 mov ecx, edx
.text:00D029C4 shrd edx, ebp, 8
.text:00D029C8 shl ecx, 18h
.text:00D029CB shr ebp, 8
.text:00D029CE or edx, eax
.text:00D029D0 or ebp, ecx ; q0 = ror(q0, 8)
.text:00D029D2 add edx, ebx
.text:00D029D4 mov ecx, esi
.text:00D029D6 adc ebp, esi ; q0 = q0 + q1
.text:00D029D8 shr ecx, 1Dh
.text:00D029DB xor ebp, [esp+144h+x01]
.text:00D029DF xor edx, edi ; q0 = q0 ^ x0
.text:00D029E1 shld esi, ebx, 3
.text:00D029E5 mov [esp+144h+d00], ebp
.text:00D029E9 or esi, eax
.text:00D029EB mov [esp+144h+d00_], ebp
.text:00D029EF xor esi, ebp
.text:00D029F1 shl ebx, 3
.text:00D029F4 mov ebp, [esp+144h+x10]
.text:00D029F8 or ebx, ecx ; q1 = rol(q1, 3)
.text:00D029FA mov ecx, [esp+144h+x11]
.text:00D029FE xor ebx, edx ; q1 = q1 ^ q0
.text:00D02A00 shrd [esp+144h+x11], ebp, 8
.text:00D02A06 or eax, [esp+144h+x11]
.text:00D02A0A shl ecx, 18h
.text:00D02A0D shr ebp, 8
.text:00D02A10 or ecx, ebp ; x1 = ror(x1, 8)
.text:00D02A12 mov [esp+144h+d01], edx
.text:00D02A16 mov ebp, [esp+144h+x01]
.text:00D02A1A add eax, edi
.text:00D02A1C mov [esp+144h+d10], esi
.text:00D02A20 adc ecx, ebp ; x1 = x1 + x0
.text:00D02A22 xor eax, dword ptr [esp+144h+i]
.text:00D02A26 xor ecx, [esp+144h+i_] ; x1 = x1 ^ i
.text:00D02A2A mov [esp+144h+x11], eax
.text:00D02A2E xor eax, eax
.text:00D02A30 mov [esp+144h+x10], ecx
.text:00D02A34 mov ecx, ebp
.text:00D02A36 shld ebp, edi, 3
.text:00D02A3A shr ecx, 1Dh
.text:00D02A3D or eax, ebp
.text:00D02A3F shl edi, 3
.text:00D02A42 xor eax, [esp+144h+x10]
.text:00D02A46 or edi, ecx ; x0 = rol(x0, 3)
.text:00D02A48 xor edi, [esp+144h+x11] ; x0 = x0 ^ x1
.text:00D02A4C mov ebp, [esp+144h+d00]
.text:00D02A50 mov [esp+144h+x01], eax
.text:00D02A54 mov eax, dword ptr [esp+144h+i]
.text:00D02A58 add eax, 1
.text:00D02A5B mov dword ptr [esp+144h+i], eax
.text:00D02A5F adc [esp+144h+i_], 0 ; i = i + 1
.text:00D02A64 jnz short loc_D02A6F
.text:00D02A66 cmp eax, 20h
.text:00D02A69 jb loc_D029C0
Вот так обрабатывается первый блок в 16 байт, далее идет такой же кусок кода, который обрабатывает последние 16 байт поксореного ключа. После чего идет обратное преобразование элементов в little endian. Все это можно представить в python как:
def encrypt_block(data):
q0, q1 = data
x0 = 0xD8E8367C058FF310
x1 = 0x16D856AF880F0E3A
for i in xrange(32):
q0 = add(ror(q0, 8), q1) ^ x0
x1 = add(ror(x1, 8), x0) ^ i
q1 = rol(q1, 3) ^ q0
x0 = rol(x0, 3) ^ x1
return q0, q1
def encrypt(data):
res = []
for i in xrange(0, len(data), 2):
res.extend(encrypt_block(data[i:i + 2]))
return res
def encrypt_passwd(passwd):
l = unpack('>4Q', pack('>16H', *passwd))
l = encrypt(l)
l = unpack('>16H', pack('>4Q', *l))
return l
Ну и выходим на финишную прямую, дальше осталась еще одна функция, которая на основе зашифрованного ключа и другого массива создаст нам финальный, который дальше и будет сравниваться с эталонным.
.text:00D01E11 push dword ptr [ebx+8]
.text:00D01E14 lea eax, [esp+128h+var_110]
.text:00D01E18 push eax
.text:00D01E19 lea eax, [esp+12Ch+var_90]
.text:00D01E20 push eax
.text:00D01E21 call mul_matrix
.text:00D01E26 mov esi, eax
.text:00D01E28 mov ecx, 20h
.text:00D01E2D rep movsd
.text:00D01E2F add esp, 0Ch
.text:00D01E32 lea edi, [esp+124h+var_110]
.text:00D01E36 mov esi, eax
.text:00D01E38 mov ecx, 20h
.text:00D01E3D rep movsd
.text:00D01E3F push dword ptr [ebx+0Ch]
.text:00D01E42 lea ecx, [esp+128h+var_110]
.text:00D01E46 call check
Как видно с названия функции она перемножает матрицы, наш массив в 16 элементов можно представить как матрицу 4x4, которая умножается на другую матрицу инициализированную в начале как и все остальные константные данные:
.text:00D01FBE mov [esp+0B4h+var_A4], 1380h
.text:00D01FC6 mov [esp+0B4h+var_A0], 0
.text:00D01FCE mov [esp+0B4h+var_9C], 4E4h
.text:00D01FD6 mov [esp+0B4h+var_98], 0
.text:00D01FDE mov [esp+0B4h+var_94], 2709h
.text:00D01FE6 mov [esp+0B4h+var_90], 0
.text:00D01FEE mov [esp+0B4h+var_8C], 2035h
.text:00D01FF6 mov [esp+0B4h+var_88], 0
.text:00D01FFE mov [esp+0B4h+var_84], 25FAh
.text:00D02006 mov [esp+0B4h+var_80], 0
.text:00D0200E mov [esp+0B4h+var_7C], 56DAh
.text:00D02016 mov [esp+0B4h+var_78], 0
.text:00D0201E mov [esp+0B4h+var_74], 103h
.text:00D02026 mov [esp+0B4h+var_70], 0
.text:00D0202E mov [esp+0B4h+var_6C], 1531h
.text:00D02036 mov [esp+0B4h+var_68], 0
.text:00D0203E mov [esp+0B4h+var_64], 0CAAh
.text:00D02046 mov [esp+0B4h+var_60], 0
.text:00D0204E mov [esp+0B4h+var_5C], 1A61h
.text:00D02056 mov [esp+0B4h+var_58], 0
.text:00D0205E mov [esp+0B4h+var_54], 0E07h
.text:00D02066 mov [esp+0B4h+var_50], 0
.text:00D0206E mov [esp+0B4h+var_4C], 20h
.text:00D02076 mov [esp+0B4h+var_48], 0
.text:00D0207E mov [esp+0B4h+var_44], 0E2h
.text:00D02086 mov [esp+0B4h+var_40], 0
.text:00D0208E mov [esp+0B4h+var_3C], 123Fh
.text:00D02096 mov [esp+0B4h+var_38], 0
.text:00D0209E mov [esp+0B4h+var_34], 0C0h
.text:00D020A9 mov [esp+0B4h+var_30], 0
.text:00D020B4 mov [esp+0B4h+var_2C], 0DC7h
.text:00D020BF mov [esp+0B4h+var_28], 0
А результат сравнивается с
.text:00D020EE mov [esp+0B4h+var_A4], 146FC26Ah
.text:00D020F6 mov [esp+0B4h+var_A0], 0
.text:00D020FE mov [esp+0B4h+var_9C], 2434019Ah
.text:00D02106 mov [esp+0B4h+var_98], 0
.text:00D0210E mov [esp+0B4h+var_94], 16B2964Eh
.text:00D02116 mov [esp+0B4h+var_90], 0
.text:00D0211E mov [esp+0B4h+var_8C], 1DFCC164h
.text:00D02126 mov [esp+0B4h+var_88], 0
.text:00D0212E mov [esp+0B4h+var_84], 10766B04h
.text:00D02136 mov [esp+0B4h+var_80], 0
.text:00D0213E mov [esp+0B4h+var_7C], 1F67E99Dh
.text:00D02146 mov [esp+0B4h+var_78], 0
.text:00D0214E mov [esp+0B4h+var_74], 13905802h
.text:00D02156 mov [esp+0B4h+var_70], 0
.text:00D0215E mov [esp+0B4h+var_6C], 14A99DA3h
.text:00D02166 mov [esp+0B4h+var_68], 0
.text:00D0216E mov [esp+0B4h+var_64], 2AE5CE6Ch
.text:00D02176 mov [esp+0B4h+var_60], 0
.text:00D0217E mov [esp+0B4h+var_5C], 4048AA7Fh
.text:00D02186 mov [esp+0B4h+var_58], 0
.text:00D0218E mov [esp+0B4h+var_54], 33CF9B5Fh
.text:00D02196 mov [esp+0B4h+var_50], 0
.text:00D0219E mov [esp+0B4h+var_4C], 2C101662h
.text:00D021A6 mov [esp+0B4h+var_48], 0
.text:00D021AE mov [esp+0B4h+var_44], 2DF5FCE4h
.text:00D021B6 mov [esp+0B4h+var_40], 0
.text:00D021BE mov [esp+0B4h+var_3C], 4C26C74Ch
.text:00D021C6 mov [esp+0B4h+var_38], 0
.text:00D021CE mov [esp+0B4h+var_34], 2CD5980Fh
.text:00D021D9 mov [esp+0B4h+var_30], 0
.text:00D021E4 mov [esp+0B4h+var_2C], 2BA9DEDBh
.text:00D021EF mov [esp+0B4h+var_28], 0
И если они равны, то ключ верен.
Зная все это можно построить схему как с это всего получить верный ключ. Сперва зная 2 матрицы нужно найти 3-ью. Для этого я использовал z3 solver
def solve():
B = []
for i in xrange(16):
B.append(Int(i))
s = Solver()
for i in B:
s.add(And(i >= 0, i <= 0xFFFF))
for i in xrange(4):
for j in xrange(4):
s.add(
B[i + 0 * 4] * A[j + 0 * 4] +
B[i + 1 * 4] * A[j + 1 * 4] +
B[i + 2 * 4] * A[j + 2 * 4] +
B[i + 3 * 4] * A[j + 3 * 4] == R[i * 4 + j]
)
r = []
if s.check() == sat:
r = []
model = s.model()
for i in xrange(16):
r.append(model[B[i]].as_long())
else:
print 'Oops'
return r
Результат этой функции, нужно расшифровать. Зная алгоритм шифрования, который не такой уж и сложный можно написать функцию дешифровки. Кроме изменения порядка операций нужно еще посчитать ключи для расшифровки, для этого достаточно сдампить их по окончанию шифрования блока. И получим такое
def decrypt_block(data):
q0, q1 = data
x0 = 0x0A728E203850A80E
x1 = 0x1B8E2679CCAEF6B4
for i in xrange(32):
x0 = ror(x0 ^ x1, 3)
q1 = ror(q1 ^ q0, 3)
x1 = rol(sub(x1 ^ (31 - i), x0), 8)
q0 = rol(sub(q0 ^ x0, q1), 8)
return q0, q1
def decrypt(data):
res = []
for i in xrange(0, len(data), 2):
res.extend(decrypt_block(data[i:i + 2]))
return res
def decrypt_passwd(passwd):
l = unpack('>4Q', pack('>16H', *passwd))
l = decrypt(l)
l = unpack('>16H', pack('>4Q', *l))
return l
И после этого остается только проксорить результат расшифровки. А все вместе это выглядит так
#!/usr/bin/env python2
from z3 import *
from struct import pack, unpack
A = [
0x1380, 0x4E4, 0x2709, 0x2035, 0x25FA, 0x56DA, 0x103, 0x1531,
0x0CAA, 0x1A61, 0x0E07, 0x20, 0x0E2, 0x123F, 0x0C0, 0x0DC7
]
R = [
0x146FC26A, 0x2434019A, 0x16B2964E, 0x1DFCC164,
0x10766B04, 0x1F67E99D, 0x13905802, 0x14A99DA3,
0x2AE5CE6C, 0x4048AA7F, 0x33CF9B5F, 0x2C101662,
0x2DF5FCE4, 0x4C26C74C, 0x2CD5980F, 0x2BA9DEDB,
]
xor_key = [
0x90DF, 0x70BC, 0x0EF57, 0x5A96, 0x0CFEE, 0x5509, 0x80CE, 0x0D20,
0x0E14F, 0x70E, 0x0A446, 0x2FC6, 0x0ECF0, 0x5355, 0x782B, 0x6457
]
def solve():
B = []
for i in xrange(16):
B.append(Int(i))
s = Solver()
for i in B:
s.add(And(i >= 0, i <= 0xFFFF))
for i in xrange(4):
for j in xrange(4):
s.add(
B[i + 0 * 4] * A[j + 0 * 4] +
B[i + 1 * 4] * A[j + 1 * 4] +
B[i + 2 * 4] * A[j + 2 * 4] +
B[i + 3 * 4] * A[j + 3 * 4] == R[i * 4 + j]
)
r = []
if s.check() == sat:
r = []
model = s.model()
for i in xrange(16):
r.append(model[B[i]].as_long())
else:
print 'Oops'
return r
def ror(n, c, bits=64):
mask = (1 << bits) - 1
return ((n >> c) | (n << (bits - c))) & mask
def rol(n, c, bits=64):
return ror(n, bits - c, bits)
def sub(n, c, bits=64):
mask = (1 << bits) - 1
return (n - c) & mask
def xor_passwd(passwd):
l = [0] * 16
for i in xrange(16):
l[i] = passwd[i] ^ xor_key[i]
return l
def decrypt_block(data):
q0, q1 = data
x0 = 0x0A728E203850A80E
x1 = 0x1B8E2679CCAEF6B4
for i in xrange(32):
x0 = ror(x0 ^ x1, 3)
q1 = ror(q1 ^ q0, 3)
x1 = rol(sub(x1 ^ (31 - i), x0), 8)
q0 = rol(sub(q0 ^ x0, q1), 8)
return q0, q1
def decrypt(data):
res = []
for i in xrange(0, len(data), 2):
res.extend(decrypt_block(data[i:i + 2]))
return res
def decrypt_passwd(passwd):
l = unpack('>4Q', pack('>16H', *passwd))
l = decrypt(l)
l = unpack('>16H', pack('>4Q', *l))
return l
passwd = solve()
passwd = decrypt_passwd(passwd)
passwd = xor_passwd(passwd)
print(''.join(map(chr, passwd)))
BKP{KYU7EC!PH3R}